causalKNN Introduction Vignette

In this vignette, we demonstrate how to use the causalKNN package to estimate heterogeneous treatment effects (with the causal KNN and treatment effect projection methods). The direct causal KNN algorithm will estimate treatment effects for our test sample. The treatment effect projection (TEP) procedure will first project a treatment effect on our training data set, and then use a regression algorithm to predict treatments effects in our test sample.

Both of these methods are introduced in Hitsch and Misra 2018 ¹. We will consider simulated data under a RCT setting with a binary treatment.

Introduction

We first provide an overview of the causal KNN and TEP algorithm and then demonstrate how to implement the estimation procedure with the package. We will consider a simulated RCT scenario with training and test data sets.

For both techniques we need to first determine the optimal K value to be used. This optimal K value will be tuned by the transformed error loss.

The causal KNN algorithm can be performed in the following steps.

For each observation in the training data set find the K nearest treated and K nearest untreated neighbors in the training data set
Estimate the conditional average treatment effect using the mean difference between the nearest treated and untreated units
Find the optimal K that yields the smallest RMSE of the CATE to the transformed outcome
For each observation in the test data set find the K nearest treated and K nearest untreated neighbors in the training data set
Compute the heterogeneous treatment effect estimates in the test set using the optimal K

The TEP procedure can also be broken down into a few steps.

For each observation in the training data set find the K nearest treated and K nearest untreated neighbors
Estimate the conditional average treatment effect using the mean difference between the nearest treated and untreated units
Find the optimal K that yields the smallest RMSE of the CATE to the transformed outcome
Compute the heterogeneous treatment effect estimates in the training set using the optimal K
Using the treatment effect estimates from the training set fit a regression model and predict on the test set

In the TEP procedure, steps 1 to 3 formulate the causal KNN regression. Step 4 performs the treatment effect projection.

This package provides a set of functions that when run sequentially will execute the steps for both methods and yield a heterogeneous treatment effect prediction for our test set. For a more “off-the-shelf” approach, the causalknn_direct wraps the direct causal KNN functions and the causalKNN_TEP wraps all the TEP functions into one.

The benefit of this estimation procedure is that once the K nearest treated and untreated neighbors index matrices are computed and stored, the subsequent steps execute relatively quickly. As a result, the initial choice of K in the first step is crucial. When in doubt, it is recommended to specify a larger K.

Estimation

We will consider simulated RCT data to demonstrate how to use the package to estimate heterogeneous treatment effects.

set.seed(1234L)
n     <-   5000  # Number of Observations in training set
p     <-   21    # Number of Features
key   <-   1:n   # Individual indices

n_test     <-   501  # Number of Observations in test set
key_test   <-   1:n_test

X     <-   cbind(matrix(rnorm(p/3*n), n, p/3),
                 matrix(5*runif(p/3*n), n, p/3),
                 matrix(rexp(p/3*n), n, p/3))

X_test           <-   matrix(0, n_test, p)
X_test[,1]       <-   rnorm(n_test)
X_test[,p/3+1]   <-   5*runif(n_test)

TE   <-   pmin(abs(X[,1] * X[,p/3+1] + 1), 4)
W    <-   rbinom(n, 1, 0.5)
Y    <-   TE * W + 5 * X[,2] + X[,3] * pmax(X[,5], 0) + 5 * sin(X[,4]) + X[,8] + rnorm(n)

Determining Optimal K

For both estimation procedures we need to first find an optimal K value.

Compute K nearest neighbors among treated and untreated

We first need to compute the K nearest neighbors index matrix for the each observation in the training set for its untreated and treated nearest neighbors. The knn_index_mat function wraps the knn.index.dist function from the KernelKnn package. This allows us to compute the KNN index matrix for a variety of possible distance metrics that are supported by the knn.index.dist function. For our example, we will use the default Euclidean distance metric.

We also need to choose how large our KNN index matrices will be (by choosing a K value). It is important to choose a K large enough that the optimal K routine down the line will have enough K values to search through. However, choosing a too large of a K value leads to a longer run time and the index matrices will take up more memory in R (as the KNN algorithm is memory-based learning).

The function is parallelized using Open MP in the back end, and we can set the number of threads to use for the nearest neighbor searching procedure.

k                 <-   120L         # Number of NN to search
distance_metric   <-   "euclidean"  # Distance metric
keep_dist         <-   FALSE        # Drop the distance matrices
threads           <-   1L           # Number of threads to use

knn_index_list    <-   knn_index_mat(X, W, k,
                                     distance_metric = distance_metric,
                                     keep_dist       = keep_dist,
                                     threads         = threads)

Finding the optimal K

Now that we have the K nearest neighbor index stored, we can compute the causal KNN treatment effects for a given K value. To find the optimal K value, we will use the knn_optimal_k function.

We will tune K based on on the transformed outcome loss or the mean squared difference between \(\hat{\tau}_K(x)\) and the transformed outcome \(Y_i^*\). The transformed outcome is defined as \[Y_i^* = \frac{W_i - e(X_i)}{e(X_i)(1-e(X_i))} Y_i\] where \(W_i\) is the observed treatment indicator, \(X_i\) is the vector of features for each individual, and \(e(X_i)\) is the estimated propensity score. Under the assumption of unconfoundedness, the transformed outcome is an unbiased estimate of the conditional average treatment effect. In our RCT setting, we know the propensity score by experimental design. The optimal K value will be the K that minimizes the transformed error loss of \(E[(Y_i^* - \hat\tau_K(X_i))^2|X_i]\).

To specify a vector of K values to search over, knn_optimal_k takes in N_step and K_step parameters. The K_step parameter determines the starting K value and the step size between K values in the vector. The N_step determines the number of total points to search over. In our example, we set N_step to \(20\) and K_step to \(5\), and this will give us a vector of K values from \(5\) to \(100\) with step increments of \(5\).

N_step   <-   20  # How many steps to take
K_step   <-   5   # Value between steps and starting value

optimal_k_list   <-   knn_optimal_k(X, W, Y, key, N_step, K_step, knn_index_list)

We can plot the RMSE of transformed error loss. As expected, we see an elbow plot when we are tuning for optimal K. By default, the knn_optimal_k function will suggest to use the K value that yields the minimum RMSE.

plot(optimal_k_list$k_vec, optimal_k_list$rmse_vec, type = "l", ylab = "RMSE", xlab = "K")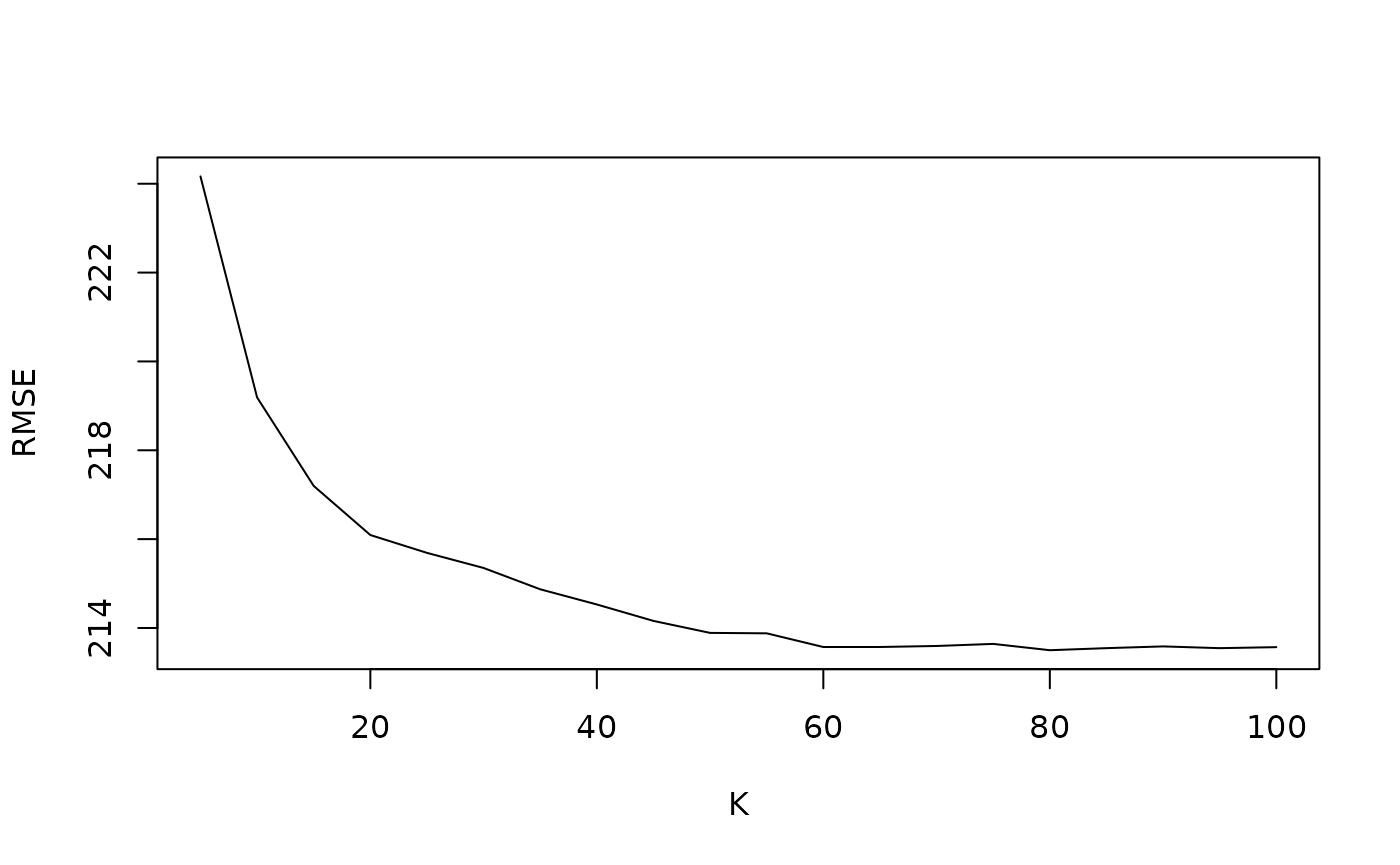

We can use the knn_optimal_k_separate function find optimal K values separately for treated and untreated nearest neighbors.

Direct Causal KNN

Now armed with our optimal K value, we can compute estimates of treatment effect on the test set with causal KNN. We first need to compute the set of K nearest neighbor matrices of our test set.

We compute the CATE by \[\hat{\tau}_K(x) = \frac{1}{K} \sum_{i \in N_k(x,1)} Y_i - \frac{1}{K} \sum_{i \in N_{K}(x,0)} Y_i\] where \(N_{K}(x,w)\) is the set of the \(K\) nearest neighbors with treatment status \(w \in \{0,1\}\) in the training sample, \(x\) is the test set features, and \(Y_i\) is the observed outcomes in the training sample.

knn_index_test_list    <-   knn_index_mat(X, W, k,
                                          DF_test         = X_test,
                                          distance_metric = distance_metric,
                                          keep_dist       = keep_dist,
                                          threads         = threads)

Then, with our pair or treated/untreated K nearest neighbor matrices of the test set to the training set, we can compute the direct causal KNN treatment effect for the test set.

causal_KNN_test_DF   <-   causalknn_treatment_effect(W, Y, key, optimal_k_list$optimal_K,
                                                     knn_index_test_list,
                                                     key_test = key_test)

Treatment Effect Projection

Causal KNN

We will first use causal KNN to get a projection of the CATE in the training set.

We similarly compute the training sample CATE by \[\hat{\tau}_K(x) = \frac{1}{K} \sum_{i \in N_k(x,1)} Y_i - \frac{1}{K} \sum_{i \in N_{K}(x,0)} Y_i\] where \(N_{K}(x,w)\) is the set of the \(K\) nearest neighbors with treatment status \(w \in \{0,1\}\), \(x\) is the features, and \(Y_i\) is the observed outcomes. We do not consider an observation to be its own nearest neighbor.

Estimate the CATE given Optimal K

Now that we have our optimal K value, we can compute the CATE for our causal KNN regression. We can call the causalknn_treatment_effect function to compute our CATE.

causal_KNN_DF   <-   causalknn_treatment_effect(W, Y, key, optimal_k_list$optimal_K, knn_index_list)

For the separate optimal K case, we can pass a vector of the K values into the causalknn_treatment_effect function, where the first element of the vector is the K for the untreated nearest neighbors and the second element of the vector is the K for the treated nearest neighbors.

Treatment Effect Regression

With the CATE estimate in the training set, we will fit a regression using our projected treatment effect estimates on the training set and then predict on the test set. More formally, we project the causal KNN treatment effect estimates \(\hat\tau_{K} (X_i)\) on to the features \(X_i\). The regression step will also allow us to regularize our causal KNN estimates. We can use any regression algorithm for causal KNN treatment effect estimates, and the package allows for an easy implementation of the Elastic-Net family of models.

Elastic Net

We will consider the Elastic-Net family of regression models for our treatment effect estimates. The tep_enet function wraps the cv.glmnet function from the glmnet package to provide a cross-validated Elastic-Net. By setting the parameter alpha to NULL, the function will also cross-validate to find the optimal alpha value. For our example, we will set alpha to \(0\) for a Ridge Regression.

TEP_results_list   <-   tep_enet(X, causal_KNN_DF$treatment_effect, X_test, alpha = 0)

“Off-the-shelf” Approach

Alternatively, we can run the all of the functions for the direct Causal KNN or the Causal KNN TEP in one step with our wrapper functions, causalKNN_direct and causalKNN_TEP.

results_list_direct   <-   causalKNN_direct(X, W, Y, key, X_test, key_test)

results_list_TEP   <-   causalKNN_TEP(X, W, Y, key, X_test, key_test,
                                      tep_e_net_options = list(alpha = 0))

If we disagree with the automatic selection of the model parameters, we can manually re-run each step given the causalKNN_TEP output.

optimal_k_list_1   <-   knn_optimal_k(X, W, Y, key, N_step, K_step, results_list_TEP$knn_index_list)

Conclusion

The causalKNN provides a set of functions to implement the direct Causal KNN regression and Causal KNN treatment effect projection (TEP). For the causal KNN regression, knn_index_mat computes nearest neighbor index matrices of treated and untreated nearest neighbors, knn_optimal_k tunes the causal KNN regression to find an optimal K value, and causalknn_treatment_effect estimates the treatment effect for a given K. The causalknn_treatment_effect function can be used to estimate treatment effects for the training or test sets. For the treatment effect projection, tep_enet fits an elastic net with the projected Causal KNN treatment effect and then predicts the treatment effects on a test set. An “off-the-shelf” approach is also possible with the causalKNN_TEP and causalKNN_TEP, but it is highly recommended for the user to consider manually tweaking the model parameters.

Hitsch, Günter J. and Misra, Sanjog, Heterogeneous Treatment Effects and Optimal Targeting Policy Evaluation (January 28, 2018). https://dx.doi.org/10.2139/ssrn.3111957 ↩︎

Walter Zhang

August 28, 2018